| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 12.1) | Exercise 12.1 | Example 4 to 6 (Before Exercise 12.2) |
| Exercise 12.2 | Example 7 to 9 (Before Exercise 12.3) | Exercise 12.3 |
| Exercise 12.4 | ||
Chapter 12 Algebraic Expressions
Welcome to the detailed solutions guide for Chapter 12: Algebraic Expressions. This chapter represents a significant development in your algebraic journey, building substantially upon the introduction to variables in Class 6 and the techniques for solving simple equations learned earlier in Class 7. The focus now shifts from finding a single unknown value in an equation to understanding the very structure and manipulation of algebraic expressions themselves. These expressions form the language of algebra, used to represent relationships, formulas, and general patterns. Mastering the skills of constructing, analyzing, and operating on these expressions is absolutely fundamental for tackling more complex algebraic problems, functions, and calculus in the future.
The solutions provided offer comprehensive explanations and step-by-step procedures for navigating the world of algebraic expressions. The exploration begins with dissecting the anatomy of an expression:
- Terms: The parts of an expression separated by addition ($+$) or subtraction ($-$) signs. For example, in $3x^2 - 5xy + 7$, the terms are $3x^2$, $-5xy$, and $7$.
- Factors: Each term is a product of its factors. Factors can be numerical or algebraic (literal). In the term $-5xy$, the factors are $-5$, $x$, and $y$.
- Coefficients: The numerical factor of a term is called its coefficient. In $3x^2$, the coefficient is $3$. In $-xy$, the coefficient is $-1$.
Solutions guide students in accurately identifying these components. Following this, expressions are classified based on the number of terms they contain:
- Monomial: An expression with only one term (e.g., $7xy$, $-5m^2$, $10$).
- Binomial: An expression with two unlike terms (e.g., $x+y$, $2a^2 - 3b$).
- Trinomial: An expression with three unlike terms (e.g., $p+q+r$, $x^2 + 2xy - y^2$).
- Polynomial: A general term for an expression with one or more terms, where the variables have non-negative integer exponents.
A absolutely crucial concept for simplification and operations is identifying Like Terms and Unlike Terms. Like terms are terms that have exactly the same algebraic (literal) factors, although their numerical coefficients may differ. For instance, $5x^2y$ and $-2x^2y$ are like terms because their algebraic factors ($x^2y$) are identical. However, $5x^2y$ and $5xy^2$ are unlike terms because their algebraic factors differ. The solutions heavily emphasize grouping like terms together, as only like terms can be combined through addition or subtraction.
The core operational focus is on Addition and Subtraction of Algebraic Expressions. Solutions detail two primary methods:
- Horizontal Method: Write the expressions in a line, remove brackets (paying attention to signs), group all like terms together, and then combine the coefficients of the like terms.
- Vertical Method: Arrange the expressions one below the other such that like terms align vertically in columns. Then, add or subtract the coefficients column by column, similar to arithmetic addition/subtraction. Solutions strongly emphasize the critical step in subtraction: change the sign of every term in the expression being subtracted before performing the column-wise addition.
Simplifying more complex expressions, potentially involving nested brackets, requires careful application of the order of operations (often remembered by acronyms like BODMAS/PEMDAS) and diligent handling of signs. Furthermore, the solutions cover finding the value of an algebraic expression for specific numerical values of its variables. This involves careful substitution of the given values (e.g., find the value of $2a - 3b^2$ when $a=5$ and $b=-2$) followed by accurate arithmetic calculation. Applications often involve substituting values into algebraic formulas for perimeter, area, or other quantities. These manipulative skills are the bedrock of advanced algebra.
Example 1 to 3 (Before Exercise 12.1)
Example 1. Identify, in the following expressions, terms which are not constants. Give their numerical coefficients:
xy + 4 , 13 – y2 , 13 – y + 5y2 , 4p2q – 3pq2 + 5
Answer:
The solution is presented in a table format below. For each expression, we identify the terms that contain variables (i.e., are not constants) and then state their corresponding numerical coefficients. The numerical coefficient is the number part of a term that is multiplied by the variable(s).
| Expression | Term (which is not a constant) | Numerical Coefficient |
| $xy + 4$ | $xy$ | 1 |
| $13 – y^2$ | $-y^2$ | -1 |
| $13 – y + 5y^2$ | $-y$ | -1 |
| $5y^2$ | 5 | |
| $4p^2q – 3pq^2 + 5$ | $4p^2q$ | 4 |
| $-3pq^2$ | -3 |
Example 2.
(a) What are the coefficients of x in the following expressions?
4x – 3y , 8 – x + y , y2x – y , 2z – 5xz
(b) What are the coefficients of y in the following expressions?
4x – 3y , 8 + yz , yz2 + 5 , my + m
Answer:
(a) Coefficients of x
The coefficient of x in a term is the remaining part of the term that multiplies x.
| Expression | Term containing x | Coefficient of x |
|---|---|---|
| $4x \ - \ 3y$ | $4x$ | 4 |
| $8 \ - \ x \ + \ y$ | $-x$ | -1 |
| $y^2x \ - \ y$ | $y^2x$ | $y^2$ |
| $2z \ - \ 5xz$ | $-5xz$ | $-5z$ |
(b) Coefficients of y
The coefficient of y in a term is the remaining part of the term that multiplies y.
| Expression | Term containing y | Coefficient of y |
|---|---|---|
| $4x \ - \ 3y$ | $-3y$ | -3 |
| $8 \ + \ yz$ | $yz$ | $z$ |
| $yz^2 \ + \ 5$ | $yz^2$ | $z^2$ |
| $my \ + \ m$ | $my$ | $m$ |
Example 3. State with reasons, which of the following pairs of terms are of like terms and which are of unlike terms:
(i) 7x , 12y
(ii) 15x , –21x
(iii) – 4ab , 7ba
(iv) 3xy , 3x
(v) 6xy2 , 9x2y
(vi) pq2 , – 4pq2
(vii) mn2 , 10mn
Answer:
Definition: Like terms are terms that have the same algebraic factors (variables raised to the same powers). Unlike terms have different algebraic factors.
| S.No. | Pair of Terms | Algebraic Factors | Like/Unlike Terms | Reason |
|---|---|---|---|---|
| (i) | $7x , 12y$ | $x$ ; $y$ | Unlike | The terms have different algebraic factors (variables). |
| (ii) | $15x , -21x$ | $x$ ; $x$ | Like | The terms have the same algebraic factor ($x$). |
| (iii) | $-4ab , 7ba$ | $a \times b$ ; $b \times a$ | Like | The terms have the same algebraic factors ($a$ and $b$). Note that $ba$ is the same as $ab$. |
| (iv) | $3xy , 3x$ | $x \times y$ ; $x$ | Unlike | The algebraic factors are different; one term has factor $y$, the other does not. |
| (v) | $6xy^2 , 9x^2y$ | $x \times y \times y$ ; $x \times x \times y$ | Unlike | The powers of the variables are different ($y^2$ vs $y$, $x$ vs $x^2$). |
| (vi) | $pq^2 , -4pq^2$ | $p \times q \times q$ ; $p \times q \times q$ | Like | The terms have the same algebraic factors ($p$ and $q^2$). |
| (vii) | $mn^2 , 10mn$ | $m \times n \times n$ ; $m \times n$ | Unlike | The powers of the variable $n$ are different ($n^2$ vs $n$). |
Exercise 12.1
Question 1. Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
(ii) One-half of the sum of numbers x and y.
(iii) The number z multiplied by itself.
(iv) One-fourth of the product of numbers p and q.
(v) Numbers x and y both squared and added.
(vi) Number 5 added to three times the product of numbers m and n.
(vii) Product of numbers y and z subtracted from 10.
(viii) Sum of numbers a and b subtracted from their product.
Answer:
(i) Subtraction of z from y
The expression is $y - z$.
(ii) One-half of the sum of numbers x and y
The sum of numbers x and y is $(x + y)$.
One-half of the sum is $\frac{1}{2}(x + y)$ or $\frac{x+y}{2}$.
(iii) The number z multiplied by itself
The expression is $z \times z = z^2$.
(iv) One-fourth of the product of numbers p and q
The product of numbers p and q is $(p \times q)$ or $pq$.
One-fourth of the product is $\frac{1}{4}(pq)$ or $\frac{pq}{4}$.
(v) Numbers x and y both squared and added
x squared is $x^2$.
y squared is $y^2$.
The expression is $x^2 + y^2$.
(vi) Number 5 added to three times the product of numbers m and n
The product of numbers m and n is $mn$.
Three times the product is $3(mn)$ or $3mn$.
Number 5 added to this is $3mn + 5$.
(vii) Product of numbers y and z subtracted from 10
The product of numbers y and z is $yz$.
Subtracting the product from 10 gives $10 - yz$.
(viii) Sum of numbers a and b subtracted from their product
The sum of numbers a and b is $(a + b)$.
The product of numbers a and b is $ab$.
Subtracting the sum from the product gives $ab - (a + b)$.
Question 2.
(i) Identify the terms and their factors in the following expressions. Show the terms and factors by tree diagrams.
(a) x – 3
(b) 1 + x + x2
(c) y – y3
(d) 5xy2 + 7x2y
(e) – ab + 2b2 – 3a2
(ii) Identify terms and factors in the expressions given below:
(a) – 4x + 5
(b) – 4x + 5y
(c) 5y + 3y2
(d) xy + 2x2y2
(e) pq + q
(f) 1.2 ab – 2.4 b + 3.6 a
(g) $\frac{3}{4}x + \frac{1}{4}$
(h) 0.1 p2 + 0.2 q2
Answer:
(i) Identification of Terms and Factors by Tree Diagrams
(a) $x – 3$
Expression: $x-3$
Terms: $x$, $-3$
Factors: $(x)$, $(-3)$
(b) $1 + x + x^2$
Expression: $1 + x + x^2$
Terms: $1$, $x$, $x^2$
Factors: $(1)$, $(x)$, $(x, x)$
(c) $y – y^3$
Expression: $y – y^3$
Terms: $y$, $-y^3$
Factors: $(y)$, $(-1, y, y, y)$
(d) $5xy^2 + 7x^2y$
Expression: $5xy^2 + 7x^2y$
Terms: $5xy^2$, $7x^2y$
Factors: $(5, x, y, y)$, $(7, x, x, y)$
(e) $– ab + 2b^2 – 3a^2$
Expression: $– ab + 2b^2 – 3a^2$
Terms: $-ab$, $2b^2$, $-3a^2$
Factors: $(-1, a, b)$, $(2, b, b)$, $(-1, 3, a, a)$
(ii) Identification of Terms and Factors in a Table
| Expression | Terms | Factors |
| (a) $– 4x + 5$ | $-4x$ | $-4, x$ |
| $5$ | $5$ | |
| (b) $– 4x + 5y$ | $-4x$ | $-4, x$ |
| $5y$ | $5, y$ | |
| (c) $5y + 3y^2$ | $5y$ | $5, y$ |
| $3y^2$ | $3, y, y$ | |
| (d) $xy + 2x^2y^2$ | $xy$ | $x, y$ |
| $2x^2y^2$ | $2, x, x, y, y$ | |
| (e) $pq + q$ | $pq$ | $p, q$ |
| $q$ | $q$ | |
| (f) $1.2 ab – 2.4 b + 3.6 a$ | $1.2ab$ | $1.2, a, b$ |
| $-2.4b$ | $-2.4, b$ | |
| $3.6a$ | $3.6, a$ | |
| (g) $\frac{3}{4}x + \frac{1}{4}$ | $\frac{3}{4}x$ | $\frac{3}{4}, x$ |
| $\frac{1}{4}$ | $\frac{1}{4}$ | |
| (h) $0.1 p^2 + 0.2 q^2$ | $0.1p^2$ | $0.1, p, p$ |
| $0.2q^2$ | $0.2, q, q$ |
Question 3. Identify the numerical coefficients of terms (other than constants) in the following expressions:
(i) 5 – 3t2
(ii) 1 + t + t2 + t3
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) –p2q2 + 7pq
(vi) 1.2 a + 0.8 b
(vii) 3.14 r2
(viii) 2 (l + b)
(ix) 0.1 y + 0.01 y2
Answer:
The following table lists the given expressions, identifies the terms which are not constants (i.e., terms containing variables), and provides their corresponding numerical coefficients.
| Expression | Term (other than constant) | Numerical Coefficient |
| (i) $5 – 3t^2$ | $-3t^2$ | -3 |
| (ii) $1 + t + t^2 + t^3$ | $t$ | 1 |
| $t^2$ | 1 | |
| $t^3$ | 1 | |
| (iii) $x + 2xy + 3y$ | $x$ | 1 |
| $2xy$ | 2 | |
| $3y$ | 3 | |
| (iv) $100m + 1000n$ | $100m$ | 100 |
| $1000n$ | 1000 | |
| (v) $–p^2q^2 + 7pq$ | $-p^2q^2$ | -1 |
| $7pq$ | 7 | |
| (vi) $1.2 a + 0.8 b$ | $1.2a$ | 1.2 |
| $0.8b$ | 0.8 | |
| (vii) $3.14 r^2$ | $3.14r^2$ | 3.14 |
| (viii) $2 (l + b) = 2l + 2b$ | $2l$ | 2 |
| $2b$ | 2 | |
| (ix) $0.1 y + 0.01 y^2$ | $0.1y$ | 0.1 |
| $0.01y^2$ | 0.01 |
Question 4.
(a) Identify terms which contain x and give the coefficient of x.
(i) y2x + y
(ii) 13y2 – 8yx
(iii) x + y + 2
(iv) 5 + z + zx
(v) 1 + x + xy
(vi) 12xy2 + 25
(vii) 7x + xy2
(b) Identify terms which contain y2 and give the coefficient of y2.
(i) 8 – xy2
(ii) 5y2 + 7x
(iii) 2x2y – 15xy2 + 7y2
Answer:
(a) Identify terms which contain x and give the coefficient of x.
The coefficient of a specific variable in a term is found by taking all other parts of the term (including the numerical coefficient and other variables) that are multiplied with it.
| Expression | Term containing 'x' | Coefficient of 'x' |
| (i) $y^2x + y$ | $y^2x$ | $y^2$ |
| (ii) $13y^2 – 8yx$ | $-8yx$ | $-8y$ |
| (iii) $x + y + 2$ | $x$ | 1 |
| (iv) $5 + z + zx$ | $zx$ | $z$ |
| (v) $1 + x + xy$ | $x$ | 1 |
| $xy$ | $y$ | |
| (vi) $12xy^2 + 25$ | $12xy^2$ | $12y^2$ |
| (vii) $7x + xy^2$ | $7x$ | 7 |
| $xy^2$ | $y^2$ |
(b) Identify terms which contain y2 and give the coefficient of y2.
Similar to the above, the coefficient of $y^2$ will be the remaining factors in the term containing $y^2$.
| Expression | Term containing 'y2' | Coefficient of 'y2' |
| (i) $8 – xy^2$ | $-xy^2$ | $-x$ |
| (ii) $5y^2 + 7x$ | $5y^2$ | 5 |
| (iii) $2x^2y – 15xy^2 + 7y^2$ | $-15xy^2$ | $-15x$ |
| $7y^2$ | 7 |
Question 5. Classify into monomials, binomials and trinomials.
(i) 4y – 7z
(ii) y2
(iii) x + y – xy
(iv) 100
(v) ab – a – b
(vi) 5 – 3t
(vii) 4p2q – 4pq2
(viii) 7mn
(ix) z2 – 3z + 8
(x) a2 + b2
(xi) z2 + z
(xii) 1 + x + x2
Answer:
We classify algebraic expressions based on the number of unlike terms they contain:
A Monomial is an expression that contains only one term.
A Binomial is an expression that contains two unlike terms.
A Trinomial is an expression that contains three unlike terms.
Based on these definitions, the classification of the given expressions is as follows:
| Expression | Number of Terms | Classification |
| (i) $4y – 7z$ | 2 | Binomial |
| (ii) $y^2$ | 1 | Monomial |
| (iii) $x + y – xy$ | 3 | Trinomial |
| (iv) $100$ | 1 | Monomial |
| (v) $ab – a – b$ | 3 | Trinomial |
| (vi) $5 – 3t$ | 2 | Binomial |
| (vii) $4p^2q – 4pq^2$ | 2 | Binomial |
| (viii) $7mn$ | 1 | Monomial |
| (ix) $z^2 – 3z + 8$ | 3 | Trinomial |
| (x) $a^2 + b^2$ | 2 | Binomial |
| (xi) $z^2 + z$ | 2 | Binomial |
| (xii) $1 + x + x^2$ | 3 | Trinomial |
Question 6. State whether a given pair of terms is of like or unlike terms.
(i) 1 , 100
(ii) –7x , $\frac{5}{2}x$
(iii) – 29x , – 29y
(iv) 14xy , 42yx
(v) 4m2p , 4mp2
(vi) 12xz , 12x2z2
Answer:
Two or more terms are considered like terms if they have the same algebraic factors. This means they must have the same variables, and each variable must have the same exponent. The numerical coefficients of like terms can be different.
Terms that do not have the same algebraic factors are called unlike terms.
The classification of the given pairs of terms is as follows:
| Pair of Terms | Algebraic Factors | Classification (Like/Unlike) |
| (i) $1, 100$ | Both are constants with no variable factors. | Like Terms |
| (ii) $–7x, \frac{5}{2}x$ | Both terms have the same algebraic factor: $x$. | Like Terms |
| (iii) $– 29x, – 29y$ | The first term has the factor $x$, and the second has the factor $y$. The factors are different. | Unlike Terms |
| (iv) $14xy, 42yx$ | Both terms have the same algebraic factors: $x$ and $y$ (since $xy = yx$). | Like Terms |
| (v) $4m^2p, 4mp^2$ | The factors are $m^2, p$ and $m, p^2$. The exponents of the variables are different. | Unlike Terms |
| (vi) $12xz, 12x^2z^2$ | The factors are $x, z$ and $x^2, z^2$. The exponents of the variables are different. | Unlike Terms |
Question 7. Identify like terms in the following:
(a) – xy2 , – 4yx2 , 8x2 , 2xy2 , 7y , – 11x2 , –100x , –11yx , 20x2y , – 6x2 , y , 2xy , 3x
(b) 10pq , 7p , 8q , – p2q2 , – 7qp , – 100q , – 23 , 12q2p2 , – 5p2 , 41 , 2405p , 78qp , 13p2q , qp2 , 701p2
Answer:
Like terms are terms that have the same variables raised to the same powers. The coefficients of the like terms can be different. We will group the like terms from the given lists.
(a) Like terms in the list:
– xy2 , – 4yx2 , 8x2 , 2xy2 , 7y , – 11x2 , –100x , –11yx , 20x2y , – 6x2 , y , 2xy , 3x
The groups of like terms are:
Group 1 (with factors $x, y^2$): $– xy^2$, $2xy^2$
Group 2 (with factors $x^2, y$): $– 4yx^2$, $20x^2y$
Group 3 (with factor $x^2$): $8x^2$, $– 11x^2$, $– 6x^2$
Group 4 (with factor $y$): $7y$, $y$
Group 5 (with factor $x$): $– 100x$, $3x$
Group 6 (with factors $x, y$): $– 11yx$, $2xy$
(b) Like terms in the list:
10pq , 7p , 8q , – p2q2 , – 7qp , – 100q , – 23 , 12q2p2 , – 5p2 , 41 , 2405p , 78qp , 13p2q , qp2 , 701p2
The groups of like terms are:
Group 1 (with factors $p, q$): $10pq$, $– 7qp$, $78qp$
Group 2 (with factor $p$): $7p$, $2405p$
Group 3 (with factor $q$): $8q$, $– 100q$
Group 4 (with factors $p^2, q^2$): $– p^2q^2$, $12q^2p^2$
Group 5 (constants): $– 23$, $41$
Group 6 (with factor $p^2$): $– 5p^2$, $701p^2$
Group 7 (with factors $p^2, q$): $13p^2q$, $qp^2$
Example 4 to 6 (Before Exercise 12.2)
Example 4. Collect like terms and simplify the expression:
12m2 – 9m + 5m – 4m2 – 7m + 10
Answer:
Given
The expression to simplify is $12m^2 – 9m + 5m – 4m^2 – 7m + 10$.
Solution
First, we identify the like terms in the expression.
Terms with $m^2$: $12m^2$ and $-4m^2$.
Terms with $m$: $-9m$, $5m$, and $-7m$.
Constant term: $10$.
Next, we rearrange the expression to group the like terms together:
$12m^2 – 4m^2 – 9m + 5m – 7m + 10$
Now, we combine the coefficients of the like terms:
Combining $m^2$ terms: $(12 - 4)m^2 = 8m^2$.
Combining $m$ terms: $(-9 + 5 - 7)m = (-4 - 7)m = -11m$.
The constant term remains $10$.
Finally, we write the simplified expression:
$8m^2 - 11m + 10$
Therefore, the simplified expression is $8m^2 - 11m + 10$.
Example 5. Subtract 24ab – 10b – 18a from 30ab + 12b + 14a.
Answer:
Given
We need to subtract the expression $(24ab – 10b – 18a)$ from the expression $(30ab + 12b + 14a)$.
This can be written as: $(30ab + 12b + 14a) - (24ab – 10b – 18a)$.
Solution (Method 1: Row Method)
To subtract, we remove the parentheses. Remember that subtracting an expression is equivalent to adding its additive inverse. So, we change the sign of each term in the expression being subtracted.
$(30ab + 12b + 14a) - (24ab – 10b – 18a)$
$= 30ab + 12b + 14a - 24ab - (-10b) - (-18a)$
$= 30ab + 12b + 14a - 24ab + 10b + 18a$
Now, we group the like terms together:
$= (30ab - 24ab) + (12b + 10b) + (14a + 18a)$
Combine the coefficients of the like terms:
$= (30 - 24)ab + (12 + 10)b + (14 + 18)a$
$= 6ab + 22b + 32a$
Therefore, the result of the subtraction is $6ab + 22b + 32a$.
Alternate Solution (Method 2: Column Method)
We arrange the expressions vertically, aligning the like terms. Then, we change the sign of each term in the expression being subtracted and add the expressions.
$\begin{array}{r} & 30ab & + & 12b & + & 14a \\ - & (24ab & - & 10b & - & 18a) \\ \hline \end{array}$
Changing the signs of the second expression and adding:
$\begin{array}{r} & 30ab & + & 12b & + & 14a \\ & -24ab & + & 10b & + & 18a \\ \hline & 6ab & + & 22b & + & 32a \\ \hline \end{array}$
The result is $6ab + 22b + 32a$.
Example 6. From the sum of 2y2 + 3yz , – y2 – yz – z2 and yz + 2z2, subtract the sum of 3y2 – z2 and – y2 + yz + z2.
Answer:
Given
First set of expressions: $(2y^2 + 3yz)$, $(-y^2 - yz - z^2)$, $(yz + 2z^2)$.
Second set of expressions: $(3y^2 - z^2)$, $(-y^2 + yz + z^2)$.
To Find
We need to find the result of subtracting the sum of the second set of expressions from the sum of the first set of expressions.
Solution
Step 1: Find the sum of the first three expressions.
Let Sum 1 be the sum of the first three expressions:
Sum 1 = $(2y^2 + 3yz) + (-y^2 - yz - z^2) + (yz + 2z^2)$
Removing parentheses:
$= 2y^2 + 3yz - y^2 - yz - z^2 + yz + 2z^2$
Grouping like terms:
$= (2y^2 - y^2) + (3yz - yz + yz) + (-z^2 + 2z^2)$
Combining like terms:
$= (2-1)y^2 + (3-1+1)yz + (-1+2)z^2$
$= y^2 + 3yz + z^2$
Step 2: Find the sum of the next two expressions.
Let Sum 2 be the sum of the next two expressions:
Sum 2 = $(3y^2 - z^2) + (-y^2 + yz + z^2)$
Removing parentheses:
$= 3y^2 - z^2 - y^2 + yz + z^2$
Grouping like terms:
$= (3y^2 - y^2) + (yz) + (-z^2 + z^2)$
Combining like terms:
$= (3-1)y^2 + yz + (-1+1)z^2$
$= 2y^2 + yz + 0z^2$
$= 2y^2 + yz$
Step 3: Subtract the second sum (Sum 2) from the first sum (Sum 1).
Result = (Sum 1) - (Sum 2)
$= (y^2 + 3yz + z^2) - (2y^2 + yz)$
Removing parentheses (change the sign of each term in the expression being subtracted):
$= y^2 + 3yz + z^2 - 2y^2 - yz$
Grouping like terms:
$= (y^2 - 2y^2) + (3yz - yz) + z^2$
Combining like terms:
$= (1 - 2)y^2 + (3 - 1)yz + z^2$
$= -y^2 + 2yz + z^2$
Therefore, the final result is $-y^2 + 2yz + z^2$.
Exercise 12.2
Question 1. Simplify combining like terms:
(i) 21b – 32 + 7b – 20b
(ii) – z2 + 13z2 – 5z + 7z3 – 15z
(iii) p – (p – q) – q – (q – p)
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
(v) 5x2y – 5x2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)
Answer:
(i) $21b – 32 + 7b – 20b$
Group the like terms:
$= (21b + 7b - 20b) - 32$
Combine the coefficients of $b$:
$= (21 + 7 - 20)b - 32$
$= (28 - 20)b - 32$
$= 8b - 32$
(ii) $– z^2 + 13z^2 – 5z + 7z^3 – 15z$
Group the like terms (usually in descending order of power):
$= 7z^3 + (-z^2 + 13z^2) + (-5z - 15z)$
Combine the coefficients:
$= 7z^3 + (-1 + 13)z^2 + (-5 - 15)z$
$= 7z^3 + 12z^2 - 20z$
(iii) $p – (p – q) – q – (q – p)$
Distribute the negative signs:
$= p - p + q - q - q + p$
Group the like terms:
$= (p - p + p) + (q - q - q)$
Combine the coefficients:
$= (1 - 1 + 1)p + (1 - 1 - 1)q$
$= 1p - 1q$
$= p - q$
(iv) $3a – 2b – ab – (a – b + ab) + 3ab + b – a$
Distribute the negative sign:
$= 3a - 2b - ab - a + b - ab + 3ab + b - a$
Group the like terms:
$= (3a - a - a) + (-2b + b + b) + (-ab - ab + 3ab)$
Combine the coefficients:
$= (3 - 1 - 1)a + (-2 + 1 + 1)b + (-1 - 1 + 3)ab$
$= (1)a + (0)b + (1)ab$
$= a + ab$
(v) $5x^2y – 5x^2 + 3yx^2 – 3y^2 + x^2 – y^2 + 8xy^2 – 3y^2$
Recognize that $yx^2$ is the same as $x^2y$. Group the like terms:
$= (5x^2y + 3yx^2) + (-5x^2 + x^2) + (-3y^2 - y^2 - 3y^2) + 8xy^2$
Combine the coefficients:
$= (5 + 3)x^2y + (-5 + 1)x^2 + (-3 - 1 - 3)y^2 + 8xy^2$
$= 8x^2y - 4x^2 - 7y^2 + 8xy^2$
(vi) $(3y^2 + 5y – 4) – (8y – y^2 – 4)$
Distribute the negative sign:
$= 3y^2 + 5y - 4 - 8y - (-y^2) - (-4)$
$= 3y^2 + 5y - 4 - 8y + y^2 + 4$
Group the like terms:
$= (3y^2 + y^2) + (5y - 8y) + (-4 + 4)$
Combine the coefficients:
$= (3 + 1)y^2 + (5 - 8)y + 0$
$= 4y^2 - 3y$
Question 2. Add:
(i) 3mn, – 5mn, 8mn, – 4mn
(ii) t – 8tz, 3tz – z, z – t
(iii) –7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
(iv) a + b – 3, b – a + 3, a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x2y, – 3xy2, –5xy2, 5x2y
(viii) 3p2q2 – 4pq + 5, – 10 p2q2, 15 + 9pq + 7p2q2
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2
Answer:
(i) Add: $3mn, – 5mn, 8mn, – 4mn$
Sum = $3mn + (-5mn) + 8mn + (-4mn)$
$= 3mn - 5mn + 8mn - 4mn$
Group the terms (all are like terms):
$= (3 - 5 + 8 - 4)mn$
$= (11 - 9)mn$
$= 2mn$
(ii) Add: $t – 8tz, 3tz – z, z – t$
Sum = $(t - 8tz) + (3tz - z) + (z - t)$
$= t - 8tz + 3tz - z + z - t$
Group like terms:
$= (t - t) + (-8tz + 3tz) + (-z + z)$
Combine coefficients:
$= (1 - 1)t + (-8 + 3)tz + (-1 + 1)z$
$= 0t - 5tz + 0z$
$= -5tz$
(iii) Add: $–7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3$
Sum = $(-7mn + 5) + (12mn + 2) + (9mn - 8) + (-2mn - 3)$
$= -7mn + 5 + 12mn + 2 + 9mn - 8 - 2mn - 3$
Group like terms:
$= (-7mn + 12mn + 9mn - 2mn) + (5 + 2 - 8 - 3)$
Combine coefficients:
$= (-7 + 12 + 9 - 2)mn + (7 - 11)$
$= (21 - 9)mn + (-4)$
$= 12mn - 4$
(iv) Add: $a + b – 3, b – a + 3, a – b + 3$
Sum = $(a + b - 3) + (b - a + 3) + (a - b + 3)$
$= a + b - 3 + b - a + 3 + a - b + 3$
Group like terms:
$= (a - a + a) + (b + b - b) + (-3 + 3 + 3)$
Combine coefficients:
$= (1 - 1 + 1)a + (1 + 1 - 1)b + (0 + 3)$
$= 1a + 1b + 3$
$= a + b + 3$
(v) Add: $14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy$
Sum = $(14x + 10y - 12xy - 13) + (18 - 7x - 10y + 8xy) + (4xy)$
$= 14x + 10y - 12xy - 13 + 18 - 7x - 10y + 8xy + 4xy$
Group like terms:
$= (14x - 7x) + (10y - 10y) + (-12xy + 8xy + 4xy) + (-13 + 18)$
Combine coefficients:
$= (14 - 7)x + (10 - 10)y + (-12 + 8 + 4)xy + (5)$
$= 7x + 0y + (-12 + 12)xy + 5$
$= 7x + 0xy + 5$
$= 7x + 5$
(vi) Add: $5m – 7n, 3n – 4m + 2, 2m – 3mn – 5$
Sum = $(5m - 7n) + (3n - 4m + 2) + (2m - 3mn - 5)$
$= 5m - 7n + 3n - 4m + 2 + 2m - 3mn - 5$
Group like terms:
$= (5m - 4m + 2m) + (-7n + 3n) - 3mn + (2 - 5)$
Combine coefficients:
$= (5 - 4 + 2)m + (-7 + 3)n - 3mn + (-3)$
$= (1 + 2)m + (-4)n - 3mn - 3$
$= 3m - 4n - 3mn - 3$
(vii) Add: $4x^2y, – 3xy^2, –5xy^2, 5x^2y$
Sum = $4x^2y + (-3xy^2) + (-5xy^2) + 5x^2y$
$= 4x^2y - 3xy^2 - 5xy^2 + 5x^2y$
Group like terms:
$= (4x^2y + 5x^2y) + (-3xy^2 - 5xy^2)$
Combine coefficients:
$= (4 + 5)x^2y + (-3 - 5)xy^2$
$= 9x^2y - 8xy^2$
(viii) Add: $3p^2q^2 – 4pq + 5, – 10 p^2q^2, 15 + 9pq + 7p^2q^2$
Sum = $(3p^2q^2 - 4pq + 5) + (-10p^2q^2) + (15 + 9pq + 7p^2q^2)$
$= 3p^2q^2 - 4pq + 5 - 10p^2q^2 + 15 + 9pq + 7p^2q^2$
Group like terms:
$= (3p^2q^2 - 10p^2q^2 + 7p^2q^2) + (-4pq + 9pq) + (5 + 15)$
Combine coefficients:
$= (3 - 10 + 7)p^2q^2 + (-4 + 9)pq + 20$
$= (10 - 10)p^2q^2 + 5pq + 20$
$= 0p^2q^2 + 5pq + 20$
$= 5pq + 20$
(ix) Add: $ab – 4a, 4b – ab, 4a – 4b$
Sum = $(ab - 4a) + (4b - ab) + (4a - 4b)$
$= ab - 4a + 4b - ab + 4a - 4b$
Group like terms:
$= (ab - ab) + (-4a + 4a) + (4b - 4b)$
Combine coefficients:
$= (1 - 1)ab + (-4 + 4)a + (4 - 4)b$
$= 0ab + 0a + 0b$
$= 0$
(x) Add: $x^2 – y^2 – 1, y^2 – 1 – x^2, 1 – x^2 – y^2$
Sum = $(x^2 - y^2 - 1) + (y^2 - 1 - x^2) + (1 - x^2 - y^2)$
$= x^2 - y^2 - 1 + y^2 - 1 - x^2 + 1 - x^2 - y^2$
Group like terms:
$= (x^2 - x^2 - x^2) + (-y^2 + y^2 - y^2) + (-1 - 1 + 1)$
Combine coefficients:
$= (1 - 1 - 1)x^2 + (-1 + 1 - 1)y^2 + (-2 + 1)$
$= -1x^2 - 1y^2 - 1$
$= -x^2 - y^2 - 1$
Question 3. Subtract:
(i) –5y2 from y2
(ii) 6xy from –12xy
(iii) (a – b) from (a + b)
(iv) a (b – 5) from b (5 – a)
(v) – m2 + 5mn from 4m2 – 3mn + 8
(vi) – x2 + 10x – 5 from 5x – 10
(vii) 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2
(viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
Answer:
(i) Subtract –5y2 from y2
Solution:
We need to calculate: $y^2 - (-5y^2)$
$= y^2 + 5y^2$
Combine like terms:
$= (1 + 5)y^2$
$= 6y^2$
The result is $6y^2$.
(ii) Subtract 6xy from –12xy
Solution:
We need to calculate: $-12xy - (6xy)$
$= -12xy - 6xy$
Combine like terms:
$= (-12 - 6)xy$
$= -18xy$
The result is $-18xy$.
(iii) Subtract (a – b) from (a + b)
Solution:
We need to calculate: $(a + b) - (a - b)$
Remove parentheses, changing signs of the second expression:
$= a + b - a - (-b)$
$= a + b - a + b$
Group like terms:
$= (a - a) + (b + b)$
Combine coefficients:
$= (1 - 1)a + (1 + 1)b$
$= 0a + 2b$
$= 2b$
The result is $2b$.
(iv) Subtract a(b – 5) from b(5 – a)
Solution:
First, expand the expressions:
$a(b - 5) = ab - 5a$
$b(5 - a) = 5b - ab$
Now, subtract $(ab - 5a)$ from $(5b - ab)$:
$(5b - ab) - (ab - 5a)$
Remove parentheses, changing signs:
$= 5b - ab - ab - (-5a)$
$= 5b - ab - ab + 5a$
Group like terms:
$= 5a + 5b + (-ab - ab)$
Combine coefficients:
$= 5a + 5b + (-1 - 1)ab$
$= 5a + 5b - 2ab$
The result is $5a + 5b - 2ab$.
(v) Subtract – m2 + 5mn from 4m2 – 3mn + 8
Solution (Row Method):
$(4m^2 - 3mn + 8) - (-m^2 + 5mn)$
Remove parentheses, changing signs:
$= 4m^2 - 3mn + 8 - (-m^2) - (5mn)$
$= 4m^2 - 3mn + 8 + m^2 - 5mn$
Group like terms:
$= (4m^2 + m^2) + (-3mn - 5mn) + 8$
Combine coefficients:
$= (4 + 1)m^2 + (-3 - 5)mn + 8$
$= 5m^2 - 8mn + 8$
Alternate Solution (Column Method):
Align like terms. Change signs of the expression to be subtracted and add.
$\begin{array}{r} & 4m^2 & - & 3mn & + & 8 \\ - & (-m^2 & + & 5mn & & ) \\ \hline \end{array}$
Change signs and add:
$\begin{array}{r} & 4m^2 & - & 3mn & + & 8 \\ & +m^2 & - & 5mn & & \\ \hline & 5m^2 & - & 8mn & + & 8 \\ \hline \end{array}$
The result is $5m^2 - 8mn + 8$.
(vi) Subtract – x2 + 10x – 5 from 5x – 10
Solution (Row Method):
$(5x - 10) - (-x^2 + 10x - 5)$
Remove parentheses, changing signs:
$= 5x - 10 - (-x^2) - (10x) - (-5)$
$= 5x - 10 + x^2 - 10x + 5$
Group like terms (in descending order of power):
$= x^2 + (5x - 10x) + (-10 + 5)$
Combine coefficients:
$= x^2 + (5 - 10)x + (-5)$
$= x^2 - 5x - 5$
Alternate Solution (Column Method):
Align like terms (use 0 for missing terms). Change signs of the expression to be subtracted and add.
$\begin{array}{r} & & & 5x & - & 10 \\ - & (-x^2 & + & 10x & - & 5) \\ \hline \end{array}$
Change signs and add:
$\begin{array}{r} & & & 5x & - & 10 \\ & +x^2 & - & 10x & + & 5 \\ \hline & x^2 & - & 5x & - & 5 \\ \hline \end{array}$
The result is $x^2 - 5x - 5$.
(vii) Subtract 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2
Solution (Row Method):
$(3ab - 2a^2 - 2b^2) - (5a^2 - 7ab + 5b^2)$
Remove parentheses, changing signs:
$= 3ab - 2a^2 - 2b^2 - 5a^2 - (-7ab) - (5b^2)$
$= 3ab - 2a^2 - 2b^2 - 5a^2 + 7ab - 5b^2$
Group like terms (e.g., by $a^2$, then $ab$, then $b^2$):
$= (-2a^2 - 5a^2) + (3ab + 7ab) + (-2b^2 - 5b^2)$
Combine coefficients:
$= (-2 - 5)a^2 + (3 + 7)ab + (-2 - 5)b^2$
$= -7a^2 + 10ab - 7b^2$
Alternate Solution (Column Method):
Align like terms. Change signs of the expression to be subtracted and add.
$\begin{array}{r} & -2a^2 & + & 3ab & - & 2b^2 \\ - & (5a^2 & - & 7ab & + & 5b^2) \\ \hline \end{array}$
Change signs and add:
$\begin{array}{r} & -2a^2 & + & 3ab & - & 2b^2 \\ & -5a^2 & + & 7ab & - & 5b^2 \\ \hline & -7a^2 & + & 10ab & - & 7b^2 \\ \hline \end{array}$
The result is $-7a^2 + 10ab - 7b^2$.
(viii) Subtract 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
Solution (Row Method):
$(5p^2 + 3q^2 - pq) - (4pq - 5q^2 - 3p^2)$
Remove parentheses, changing signs:
$= 5p^2 + 3q^2 - pq - 4pq - (-5q^2) - (-3p^2)$
$= 5p^2 + 3q^2 - pq - 4pq + 5q^2 + 3p^2$
Group like terms (e.g., by $p^2$, then $q^2$, then $pq$):
$= (5p^2 + 3p^2) + (3q^2 + 5q^2) + (-pq - 4pq)$
Combine coefficients:
$= (5 + 3)p^2 + (3 + 5)q^2 + (-1 - 4)pq$
$= 8p^2 + 8q^2 - 5pq$
Alternate Solution (Column Method):
Align like terms. Change signs of the expression to be subtracted and add.
$\begin{array}{r} & 5p^2 & + & 3q^2 & - & pq \\ - & (-3p^2 & - & 5q^2 & + & 4pq) \\ \hline \end{array}$
Change signs and add:
$\begin{array}{r} & 5p^2 & + & 3q^2 & - & pq \\ & +3p^2 & + & 5q^2 & - & 4pq \\ \hline & 8p^2 & + & 8q^2 & - & 5pq \\ \hline \end{array}$
The result is $8p^2 + 8q^2 - 5pq$.
Question 4.
(a) What should be added to x2 + xy + y2 to obtain 2x2 + 3xy?
(b) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
Answer:
(a) What should be added to $x^2 + xy + y^2$ to obtain $2x^2 + 3xy$?
Given
Initial expression: $x^2 + xy + y^2$
Target expression: $2x^2 + 3xy$
To Find
The expression that should be added to the initial expression to get the target expression.
Solution
Let the required expression be $P$.
According to the problem, $(x^2 + xy + y^2) + P = 2x^2 + 3xy$.
To find $P$, we subtract $(x^2 + xy + y^2)$ from $(2x^2 + 3xy)$.
$P = (2x^2 + 3xy) - (x^2 + xy + y^2)$
Remove the parentheses, changing the sign of each term being subtracted:
$P = 2x^2 + 3xy - x^2 - xy - y^2$
Group the like terms:
$P = (2x^2 - x^2) + (3xy - xy) - y^2$
Combine the coefficients:
$P = (2 - 1)x^2 + (3 - 1)xy - y^2$
$P = x^2 + 2xy - y^2$
Therefore, $x^2 + 2xy - y^2$ should be added to $x^2 + xy + y^2$ to obtain $2x^2 + 3xy$.
(b) What should be subtracted from $2a + 8b + 10$ to get $– 3a + 7b + 16$?
Given
Initial expression: $2a + 8b + 10$
Resulting expression: $-3a + 7b + 16$
To Find
The expression that should be subtracted from the initial expression to get the resulting expression.
Solution
Let the required expression be $Q$.
According to the problem, $(2a + 8b + 10) - Q = -3a + 7b + 16$.
To find $Q$, we subtract the resulting expression $(-3a + 7b + 16)$ from the initial expression $(2a + 8b + 10)$.
$Q = (2a + 8b + 10) - (-3a + 7b + 16)$
Remove the parentheses, changing the sign of each term being subtracted:
$Q = 2a + 8b + 10 - (-3a) - (7b) - (16)$
$Q = 2a + 8b + 10 + 3a - 7b - 16$
Group the like terms:
$Q = (2a + 3a) + (8b - 7b) + (10 - 16)$
Combine the coefficients:
$Q = (2 + 3)a + (8 - 7)b + (-6)$
$Q = 5a + 1b - 6$
$Q = 5a + b - 6$
Therefore, $5a + b - 6$ should be subtracted from $2a + 8b + 10$ to get $-3a + 7b + 16$.
Question 5. What should be taken away from 3x2 – 4y2 + 5xy + 20 to obtain – x2 – y2 + 6xy + 20?
Answer:
Given
The initial expression: $3x^2 – 4y^2 + 5xy + 20$
The resulting expression: $- x^2 – y^2 + 6xy + 20$
To Find
The expression that should be "taken away" (subtracted) from the initial expression to get the resulting expression.
Solution
Let the expression to be taken away be $P$.
According to the problem, we have:
$(3x^2 – 4y^2 + 5xy + 20) - P = (– x^2 – y^2 + 6xy + 20)$
To find $P$, we need to subtract the resulting expression from the initial expression:
$P = (3x^2 – 4y^2 + 5xy + 20) - (– x^2 – y^2 + 6xy + 20)$
Remove the parentheses, remembering to change the sign of each term in the expression being subtracted:
$P = 3x^2 – 4y^2 + 5xy + 20 - (-x^2) - (-y^2) - (6xy) - (20)$
$P = 3x^2 – 4y^2 + 5xy + 20 + x^2 + y^2 - 6xy - 20$
Now, group the like terms together:
$P = (3x^2 + x^2) + (– 4y^2 + y^2) + (5xy - 6xy) + (20 - 20)$
Combine the coefficients of the like terms:
$P = (3 + 1)x^2 + (– 4 + 1)y^2 + (5 - 6)xy + 0$
$P = 4x^2 + (– 3)y^2 + (– 1)xy$
$P = 4x^2 - 3y^2 - xy$
Therefore, the expression that should be taken away is $4x^2 - 3y^2 - xy$.
Question 6.
(a) From the sum of 3x – y + 11 and – y – 11, subtract 3x – y – 11.
(b) From the sum of 4 + 3x and 5 – 4x + 2x2, subtract the sum of 3x2 – 5x and –x2 + 2x + 5.
Answer:
(a) From the sum of $3x – y + 11$ and $– y – 11$, subtract $3x – y – 11$.
Solution
Step 1: Find the sum of the first two expressions.
Sum = $(3x - y + 11) + (-y - 11)$
Remove parentheses:
$= 3x - y + 11 - y - 11$
Group like terms:
$= 3x + (-y - y) + (11 - 11)$
Combine coefficients:
$= 3x + (-1 - 1)y + 0$
$= 3x - 2y$
So, the sum of the first two expressions is $3x - 2y$.
Step 2: Subtract the third expression from the sum found in Step 1.
Result = (Sum from Step 1) - (Third expression)
$= (3x - 2y) - (3x - y - 11)$
Remove parentheses, changing the signs of the terms being subtracted:
$= 3x - 2y - 3x - (-y) - (-11)$
$= 3x - 2y - 3x + y + 11$
Group like terms:
$= (3x - 3x) + (-2y + y) + 11$
Combine coefficients:
$= (3 - 3)x + (-2 + 1)y + 11$
$= 0x + (-1)y + 11$
$= -y + 11$
Therefore, the final result for part (a) is $-y + 11$.
(b) From the sum of $4 + 3x$ and $5 – 4x + 2x^2$, subtract the sum of $3x^2 – 5x$ and $–x^2 + 2x + 5$.
Solution
Step 1: Find the sum of the first pair of expressions.
Sum 1 = $(4 + 3x) + (5 - 4x + 2x^2)$
Remove parentheses and group like terms (in descending order of power):
$= 2x^2 + (3x - 4x) + (4 + 5)$
Combine coefficients:
$= 2x^2 + (3 - 4)x + 9$
$= 2x^2 - x + 9$
Step 2: Find the sum of the second pair of expressions.
Sum 2 = $(3x^2 - 5x) + (-x^2 + 2x + 5)$
Remove parentheses and group like terms:
$= (3x^2 - x^2) + (-5x + 2x) + 5$
Combine coefficients:
$= (3 - 1)x^2 + (-5 + 2)x + 5$
$= 2x^2 - 3x + 5$
Step 3: Subtract the second sum (Sum 2) from the first sum (Sum 1).
Result = (Sum 1) - (Sum 2)
$= (2x^2 - x + 9) - (2x^2 - 3x + 5)$
Remove parentheses, changing the signs of the terms in Sum 2:
$= 2x^2 - x + 9 - 2x^2 - (-3x) - 5$
$= 2x^2 - x + 9 - 2x^2 + 3x - 5$
Group like terms:
$= (2x^2 - 2x^2) + (-x + 3x) + (9 - 5)$
Combine coefficients:
$= (2 - 2)x^2 + (-1 + 3)x + 4$
$= 0x^2 + 2x + 4$
$= 2x + 4$
Therefore, the final result for part (b) is $2x + 4$.
Example 7 to 9 (Before Exercise 12.3)
Example 7. Find the values of the following expressions for x = 2.
(i) x + 4
(ii) 4x – 3
(iii) 19 – 5x2
(iv) 100 – 10x3
Answer:
We are asked to find the value of the given expressions when the variable $x$ is equal to $2$.
(i) Expression: $x + 4$
Solution:
Substitute $x = 2$ into the expression:
Value $= 2 + 4$
Value $= 6$
Therefore, the value of $x + 4$ when $x=2$ is 6.
(ii) Expression: $4x – 3$
Solution:
Substitute $x = 2$ into the expression:
Value $= 4(2) - 3$
$= 8 - 3$
$= 5$
Therefore, the value of $4x - 3$ when $x=2$ is 5.
(iii) Expression: $19 – 5x^2$
Solution:
Substitute $x = 2$ into the expression:
Value $= 19 - 5(2)^2$
First, calculate the power:
$= 19 - 5(4)$
Next, perform the multiplication:
$= 19 - 20$
Finally, perform the subtraction:
$= -1$
Therefore, the value of $19 - 5x^2$ when $x=2$ is -1.
(iv) Expression: $100 – 10x^3$
Solution:
Substitute $x = 2$ into the expression:
Value $= 100 - 10(2)^3$
First, calculate the power:
$= 100 - 10(8)$
Next, perform the multiplication:
$= 100 - 80$
Finally, perform the subtraction:
$= 20$
Therefore, the value of $100 - 10x^3$ when $x=2$ is 20.
Example 8. Find the value of the following expressions when n = – 2.
(i) 5n – 2
(ii) 5n2 + 5n – 2
(iii) n3 + 5n2 + 5n – 2
Answer:
We are asked to find the value of the given expressions when the variable $n$ is equal to $-2$.
(i) Expression: $5n - 2$
Solution:
Substitute $n = -2$ into the expression:
Value $= 5(-2) - 2$
Perform the multiplication:
$= -10 - 2$
Perform the subtraction:
$= -12$
Therefore, the value of $5n - 2$ when $n=-2$ is $-12$.
(ii) Expression: $5n^2 + 5n - 2$
Solution:
Substitute $n = -2$ into the expression:
Value $= 5(-2)^2 + 5(-2) - 2$
First, calculate the power: $(-2)^2 = 4$.
$= 5(4) + 5(-2) - 2$
Next, perform the multiplications:
$= 20 + (-10) - 2$
$= 20 - 10 - 2$
Perform the subtractions from left to right:
$= 10 - 2$
$= 8$
Therefore, the value of $5n^2 + 5n - 2$ when $n=-2$ is $8$.
(iii) Expression: $n^3 + 5n^2 + 5n - 2$
Solution:
Substitute $n = -2$ into the expression:
Value $= (-2)^3 + 5(-2)^2 + 5(-2) - 2$
First, calculate the powers: $(-2)^3 = -8$ and $(-2)^2 = 4$.
$= (-8) + 5(4) + 5(-2) - 2$
Next, perform the multiplications:
$= -8 + 20 + (-10) - 2$
$= -8 + 20 - 10 - 2$
Perform the additions and subtractions from left to right:
$= 12 - 10 - 2$
$= 2 - 2$
$= 0$
Therefore, the value of $n^3 + 5n^2 + 5n - 2$ when $n=-2$ is $0$.
Example 9. Find the value of the following expressions for a = 3, b = 2.
(i) a + b
(ii) 7a – 4b
(iii) a2 + 2ab + b2
(iv) a3 – b3
Answer:
Given
The values of the variables are $a = 3$ and $b = 2$.
To Find
The value of the given expressions by substituting the values of $a$ and $b$.
(i) Expression: $a + b$
Solution:
Substitute $a = 3$ and $b = 2$ into the expression:
Value $= 3 + 2$
Value $= 5$
Therefore, the value of $a + b$ when $a=3$ and $b=2$ is 5.
(ii) Expression: $7a – 4b$
Solution:
Substitute $a = 3$ and $b = 2$ into the expression:
Value $= 7(3) - 4(2)$
Perform the multiplications:
$= 21 - 8$
Perform the subtraction:
$= 13$
Therefore, the value of $7a - 4b$ when $a=3$ and $b=2$ is 13.
(iii) Expression: $a^2 + 2ab + b^2$
Solution:
Substitute $a = 3$ and $b = 2$ into the expression:
Value $= (3)^2 + 2(3)(2) + (2)^2$
Calculate the powers and the multiplication:
$= 9 + 12 + 4$
Perform the additions:
$= 21 + 4$
$= 25$
Therefore, the value of $a^2 + 2ab + b^2$ when $a=3$ and $b=2$ is 25.
Alternate Method: Recognize that $a^2 + 2ab + b^2 = (a+b)^2$.
Value $= (3+2)^2 = (5)^2 = 25$.
(iv) Expression: $a^3 – b^3$
Solution:
Substitute $a = 3$ and $b = 2$ into the expression:
Value $= (3)^3 - (2)^3$
Calculate the powers:
$= 27 - 8$
Perform the subtraction:
$= 19$
Therefore, the value of $a^3 - b^3$ when $a=3$ and $b=2$ is 19.
Exercise 12.3
Question 1. If m = 2, find the value of:
(i) m – 2
(ii) 3m – 5
(iii) 9 – 5m
(iv) 3m2 – 2m – 7
(v) $\frac{5m}{2} - 4$
Answer:
Given
The value of the variable $m$ is $2$.
To Find
The value of the given expressions by substituting $m = 2$.
(i) Expression: $m - 2$
Solution:
Substitute $m = 2$ into the expression:
Value $= 2 - 2$
Value $= 0$
Therefore, the value of $m - 2$ when $m=2$ is 0.
(ii) Expression: $3m - 5$
Solution:
Substitute $m = 2$ into the expression:
Value $= 3(2) - 5$
Perform the multiplication:
$= 6 - 5$
Perform the subtraction:
$= 1$
Therefore, the value of $3m - 5$ when $m=2$ is 1.
(iii) Expression: $9 - 5m$
Solution:
Substitute $m = 2$ into the expression:
Value $= 9 - 5(2)$
Perform the multiplication:
$= 9 - 10$
Perform the subtraction:
$= -1$
Therefore, the value of $9 - 5m$ when $m=2$ is -1.
(iv) Expression: $3m^2 - 2m - 7$
Solution:
Substitute $m = 2$ into the expression:
Value $= 3(2)^2 - 2(2) - 7$
Calculate the power: $(2)^2 = 4$.
$= 3(4) - 2(2) - 7$
Perform the multiplications:
$= 12 - 4 - 7$
Perform the subtractions from left to right:
$= 8 - 7$
$= 1$
Therefore, the value of $3m^2 - 2m - 7$ when $m=2$ is 1.
(v) Expression: $\frac{5m}{2} - 4$
Solution:
Substitute $m = 2$ into the expression:
Value $= \frac{5(2)}{2} - 4$
Perform the multiplication in the numerator:
$= \frac{10}{2} - 4$
Perform the division (or cancel the 2s):
$= 5 - 4$
Perform the subtraction:
$= 1$
Therefore, the value of $\frac{5m}{2} - 4$ when $m=2$ is 1.
Question 2. If p = – 2, find the value of:
(i) 4p + 7
(ii) – 3p2 + 4p + 7
(iii) – 2p3 – 3p2 + 4p + 7
Answer:
Given
The value of the variable $p$ is $-2$.
To Find
The value of the given expressions by substituting $p = -2$.
(i) Expression: $4p + 7$
Solution:
Substitute $p = -2$ into the expression:
Value $= 4(-2) + 7$
Perform the multiplication:
$= -8 + 7$
Perform the addition:
$= -1$
Therefore, the value of $4p + 7$ when $p=-2$ is -1.
(ii) Expression: $– 3p^2 + 4p + 7$
Solution:
Substitute $p = -2$ into the expression:
Value $= -3(-2)^2 + 4(-2) + 7$
First, calculate the power: $(-2)^2 = 4$.
$= -3(4) + 4(-2) + 7$
Perform the multiplications:
$= -12 + (-8) + 7$
$= -12 - 8 + 7$
Perform the addition/subtraction from left to right:
$= -20 + 7$
$= -13$
Therefore, the value of $– 3p^2 + 4p + 7$ when $p=-2$ is -13.
(iii) Expression: $– 2p^3 – 3p^2 + 4p + 7$
Solution:
Substitute $p = -2$ into the expression:
Value $= -2(-2)^3 - 3(-2)^2 + 4(-2) + 7$
First, calculate the powers: $(-2)^3 = -8$ and $(-2)^2 = 4$.
$= -2(-8) - 3(4) + 4(-2) + 7$
Perform the multiplications:
$= 16 - 12 + (-8) + 7$
$= 16 - 12 - 8 + 7$
Perform the addition/subtraction from left to right:
$= 4 - 8 + 7$
$= -4 + 7$
$= 3$
Therefore, the value of $– 2p^3 – 3p^2 + 4p + 7$ when $p=-2$ is 3.
Question 3. Find the value of the following expressions, when x = –1:
(i) 2x – 7
(ii) – x + 2
(iii) x2 + 2x + 1
(iv) 2x2 – x – 2
Answer:
Given
The value of the variable $x$ is $-1$.
To Find
The value of the given expressions by substituting $x = -1$.
(i) Expression: $2x - 7$
Solution:
Substitute $x = -1$ into the expression:
Value $= 2(-1) - 7$
Perform the multiplication:
$= -2 - 7$
Perform the subtraction:
$= -9$
Therefore, the value of $2x - 7$ when $x=-1$ is -9.
(ii) Expression: $– x + 2$
Solution:
Substitute $x = -1$ into the expression:
Value $= -(-1) + 2$
Simplify the double negative:
$= 1 + 2$
Perform the addition:
$= 3$
Therefore, the value of $– x + 2$ when $x=-1$ is 3.
(iii) Expression: $x^2 + 2x + 1$
Solution:
Substitute $x = -1$ into the expression:
Value $= (-1)^2 + 2(-1) + 1$
Calculate the power: $(-1)^2 = 1$.
$= 1 + 2(-1) + 1$
Perform the multiplication:
$= 1 - 2 + 1$
Perform the addition/subtraction from left to right:
$= -1 + 1$
$= 0$
Therefore, the value of $x^2 + 2x + 1$ when $x=-1$ is 0.
(Alternatively, note that $x^2 + 2x + 1 = (x+1)^2$. Substituting $x=-1$ gives $(-1+1)^2 = 0^2 = 0$.)
(iv) Expression: $2x^2 – x – 2$
Solution:
Substitute $x = -1$ into the expression:
Value $= 2(-1)^2 - (-1) - 2$
Calculate the power: $(-1)^2 = 1$.
$= 2(1) - (-1) - 2$
Perform the multiplication and simplify the double negative:
$= 2 + 1 - 2$
Perform the addition/subtraction from left to right:
$= 3 - 2$
$= 1$
Therefore, the value of $2x^2 – x – 2$ when $x=-1$ is 1.
Question 4. If a = 2, b = – 2, find the value of:
(i) a2 + b2
(ii) a2 + ab + b2
(iii) a2 – b2
Answer:
Given
The values of the variables are $a = 2$ and $b = -2$.
To Find
The value of the given expressions by substituting $a = 2$ and $b = -2$.
(i) Expression: $a^2 + b^2$
Solution:
Substitute $a = 2$ and $b = -2$ into the expression:
Value $= (2)^2 + (-2)^2$
Calculate the powers:
$= 4 + 4$
Perform the addition:
$= 8$
Therefore, the value of $a^2 + b^2$ when $a=2$ and $b=-2$ is 8.
(ii) Expression: $a^2 + ab + b^2$
Solution:
Substitute $a = 2$ and $b = -2$ into the expression:
Value $= (2)^2 + (2)(-2) + (-2)^2$
Calculate the powers and the multiplication:
$= 4 + (-4) + 4$
$= 4 - 4 + 4$
Perform the addition/subtraction from left to right:
$= 0 + 4$
$= 4$
Therefore, the value of $a^2 + ab + b^2$ when $a=2$ and $b=-2$ is 4.
(iii) Expression: $a^2 - b^2$
Solution:
Substitute $a = 2$ and $b = -2$ into the expression:
Value $= (2)^2 - (-2)^2$
Calculate the powers:
$= 4 - 4$
Perform the subtraction:
$= 0$
Therefore, the value of $a^2 - b^2$ when $a=2$ and $b=-2$ is 0.
Question 5. When a = 0, b = – 1, find the value of the given expressions:
(i) 2a + 2b
(ii) 2a2 + b2 + 1
(iii) 2a2b + 2ab2 + ab
(iv) a2 + ab + 2
Answer:
Given
The values of the variables are $a = 0$ and $b = -1$.
To Find
The value of the given expressions by substituting $a = 0$ and $b = -1$.
(i) Expression: $2a + 2b$
Solution:
Substitute $a = 0$ and $b = -1$ into the expression:
Value $= 2(0) + 2(-1)$
Perform the multiplications:
$= 0 + (-2)$
$= -2$
Therefore, the value of $2a + 2b$ when $a=0$ and $b=-1$ is -2.
(ii) Expression: $2a^2 + b^2 + 1$
Solution:
Substitute $a = 0$ and $b = -1$ into the expression:
Value $= 2(0)^2 + (-1)^2 + 1$
Calculate the powers: $(0)^2 = 0$ and $(-1)^2 = 1$.
$= 2(0) + 1 + 1$
Perform the multiplication:
$= 0 + 1 + 1$
Perform the additions:
$= 2$
Therefore, the value of $2a^2 + b^2 + 1$ when $a=0$ and $b=-1$ is 2.
(iii) Expression: $2a^2b + 2ab^2 + ab$
Solution:
Substitute $a = 0$ and $b = -1$ into the expression:
Value $= 2(0)^2(-1) + 2(0)(-1)^2 + (0)(-1)$
Calculate the powers: $(0)^2 = 0$ and $(-1)^2 = 1$.
$= 2(0)(-1) + 2(0)(1) + (0)(-1)$
Perform the multiplications. Since each term contains a factor of 0, each term becomes 0.
$= 0 + 0 + 0$
$= 0$
Therefore, the value of $2a^2b + 2ab^2 + ab$ when $a=0$ and $b=-1$ is 0.
(iv) Expression: $a^2 + ab + 2$
Solution:
Substitute $a = 0$ and $b = -1$ into the expression:
Value $= (0)^2 + (0)(-1) + 2$
Calculate the power and the multiplication:
$= 0 + 0 + 2$
Perform the addition:
$= 2$
Therefore, the value of $a^2 + ab + 2$ when $a=0$ and $b=-1$ is 2.
Question 6. Simplify the expressions and find the value if x is equal to 2
(i) x + 7 + 4 (x – 5)
(ii) 3 (x + 2) + 5x – 7
(iii) 6x + 5 (x – 2)
(iv) 4(2x – 1) + 3x + 11
Answer:
Given
The value of the variable $x$ is $2$.
To Find
First, simplify each expression. Then, find the value of the simplified expression by substituting $x = 2$.
(i) Expression: $x + 7 + 4(x - 5)$
Simplification:
Distribute the 4:
$= x + 7 + 4x - 4(5)$
$= x + 7 + 4x - 20$
Group like terms:
$= (x + 4x) + (7 - 20)$
Combine like terms:
$= 5x - 13$
Finding the value (substitute $x = 2$ into $5x - 13$):
Value $= 5(2) - 13$
$= 10 - 13$
$= -3$
The simplified expression is $5x - 13$ and its value when $x=2$ is -3.
(ii) Expression: $3(x + 2) + 5x - 7$
Simplification:
Distribute the 3:
$= 3x + 3(2) + 5x - 7$
$= 3x + 6 + 5x - 7$
Group like terms:
$= (3x + 5x) + (6 - 7)$
Combine like terms:
$= 8x - 1$
Finding the value (substitute $x = 2$ into $8x - 1$):
Value $= 8(2) - 1$
$= 16 - 1$
$= 15$
The simplified expression is $8x - 1$ and its value when $x=2$ is 15.
(iii) Expression: $6x + 5(x - 2)$
Simplification:
Distribute the 5:
$= 6x + 5x - 5(2)$
$= 6x + 5x - 10$
Combine like terms:
$= (6 + 5)x - 10$
$= 11x - 10$
Finding the value (substitute $x = 2$ into $11x - 10$):
Value $= 11(2) - 10$
$= 22 - 10$
$= 12$
The simplified expression is $11x - 10$ and its value when $x=2$ is 12.
(iv) Expression: $4(2x - 1) + 3x + 11$
Simplification:
Distribute the 4:
$= 4(2x) - 4(1) + 3x + 11$
$= 8x - 4 + 3x + 11$
Group like terms:
$= (8x + 3x) + (-4 + 11)$
Combine like terms:
$= 11x + 7$
Finding the value (substitute $x = 2$ into $11x + 7$):
Value $= 11(2) + 7$
$= 22 + 7$
$= 29$
The simplified expression is $11x + 7$ and its value when $x=2$ is 29.
Question 7. Simplify these expressions and find their values if x = 3, a = – 1, b = – 2.
(i) 3x – 5 – x + 9
(ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1
(iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a
Answer:
Given
The values of the variables are $x = 3$, $a = -1$, $b = -2$.
To Find
First, simplify each expression. Then, find the value of the simplified expression by substituting the given variable values.
(i) Expression: $3x – 5 – x + 9$
Simplification:
Group like terms:
$= (3x - x) + (-5 + 9)$
Combine coefficients:
$= (3 - 1)x + 4$
$= 2x + 4$
Finding the value (substitute $x = 3$ into $2x + 4$):
Value $= 2(3) + 4$
$= 6 + 4$
$= 10$
The simplified expression is $2x + 4$ and its value is 10.
(ii) Expression: $2 – 8x + 4x + 4$
Simplification:
Group like terms:
$= (-8x + 4x) + (2 + 4)$
Combine coefficients:
$= (-8 + 4)x + 6$
$= -4x + 6$
Finding the value (substitute $x = 3$ into $-4x + 6$):
Value $= -4(3) + 6$
$= -12 + 6$
$= -6$
The simplified expression is $-4x + 6$ and its value is -6.
(iii) Expression: $3a + 5 – 8a + 1$
Simplification:
Group like terms:
$= (3a - 8a) + (5 + 1)$
Combine coefficients:
$= (3 - 8)a + 6$
$= -5a + 6$
Finding the value (substitute $a = -1$ into $-5a + 6$):
Value $= -5(-1) + 6$
$= 5 + 6$
$= 11$
The simplified expression is $-5a + 6$ and its value is 11.
(iv) Expression: $10 – 3b – 4 – 5b$
Simplification:
Group like terms:
$= (-3b - 5b) + (10 - 4)$
Combine coefficients:
$= (-3 - 5)b + 6$
$= -8b + 6$
Finding the value (substitute $b = -2$ into $-8b + 6$):
Value $= -8(-2) + 6$
$= 16 + 6$
$= 22$
The simplified expression is $-8b + 6$ and its value is 22.
(v) Expression: $2a – 2b – 4 – 5 + a$
Simplification:
Group like terms:
$= (2a + a) - 2b + (-4 - 5)$
Combine coefficients:
$= (2 + 1)a - 2b - 9$
$= 3a - 2b - 9$
Finding the value (substitute $a = -1, b = -2$ into $3a - 2b - 9$):
Value $= 3(-1) - 2(-2) - 9$
$= -3 - (-4) - 9$
$= -3 + 4 - 9$
$= 1 - 9$
$= -8$
The simplified expression is $3a - 2b - 9$ and its value is -8.
Question 8.
(i) If z = 10, find the value of z3 – 3(z – 10)
(ii) If p = – 10, find the value of p2 – 2p – 100
Answer:
(i) If $z = 10$, find the value of $z^3 - 3(z - 10)$
Given:
The value of the variable $z$ is $10$.
The expression is $z^3 - 3(z - 10)$.
Solution:
Substitute $z = 10$ into the expression:
Value $= (10)^3 - 3(10 - 10)$
First, evaluate the expression inside the parentheses and the power:
$10 - 10 = 0$
$(10)^3 = 10 \times 10 \times 10 = 1000$
Substitute these back into the expression:
Value $= 1000 - 3(0)$
Perform the multiplication:
$= 1000 - 0$
Perform the subtraction:
$= 1000$
Therefore, the value of $z^3 - 3(z - 10)$ when $z=10$ is 1000.
(ii) If $p = – 10$, find the value of $p^2 - 2p - 100$
Given:
The value of the variable $p$ is $-10$.
The expression is $p^2 - 2p - 100$.
Solution:
Substitute $p = -10$ into the expression:
Value $= (-10)^2 - 2(-10) - 100$
First, calculate the power: $(-10)^2 = (-10) \times (-10) = 100$.
Perform the multiplications:
$= 100 - (-20) - 100$
Simplify the double negative:
$= 100 + 20 - 100$
Perform the addition/subtraction from left to right:
$= 120 - 100$
$= 20$
Therefore, the value of $p^2 - 2p - 100$ when $p=-10$ is 20.
Question 9. What should be the value of a if the value of 2x2 + x – a equals to 5, when x = 0?
Answer:
Given
The expression is $2x^2 + x - a$.
The value of the expression is $5$ when $x = 0$.
To Find
The value of the constant $a$.
Solution
We are given the equation:
$2x^2 + x - a = 5$
We need to find the value of $a$ when $x = 0$.
Substitute $x = 0$ into the equation:
$2(0)^2 + (0) - a = 5$
Calculate the terms involving $x$:
$2(0) + 0 - a = 5$
$0 + 0 - a = 5$
$-a = 5$
To find $a$, multiply both sides by $-1$:
$a = -5$
Therefore, the value of $a$ should be -5 for the expression $2x^2 + x - a$ to equal 5 when $x = 0$.
Question 10. Simplify the expression and find its value when a = 5 and b = – 3.
2(a2 + ab) + 3 – ab
Answer:
Given
The expression is $2(a^2 + ab) + 3 – ab$.
The values of the variables are $a = 5$ and $b = -3$.
To Find
1. Simplify the given expression.
2. Find the value of the simplified expression using the given values of $a$ and $b$.
Solution
Step 1: Simplify the expression $2(a^2 + ab) + 3 – ab$
First, distribute the 2 into the parentheses:
$= 2(a^2) + 2(ab) + 3 - ab$
$= 2a^2 + 2ab + 3 - ab$
Next, group the like terms (the terms containing $ab$):
$= 2a^2 + (2ab - ab) + 3$
Combine the like terms:
$= 2a^2 + (2 - 1)ab + 3$
$= 2a^2 + 1ab + 3$
$= 2a^2 + ab + 3$
The simplified expression is $2a^2 + ab + 3$.
Step 2: Find the value of the simplified expression when $a = 5$ and $b = -3$
Substitute $a = 5$ and $b = -3$ into the simplified expression $2a^2 + ab + 3$:
Value $= 2(5)^2 + (5)(-3) + 3$
Calculate the power: $(5)^2 = 25$.
$= 2(25) + (5)(-3) + 3$
Perform the multiplications:
$= 50 + (-15) + 3$
$= 50 - 15 + 3$
Perform the subtraction and addition from left to right:
$= 35 + 3$
$= 38$
Therefore, the value of the expression when $a = 5$ and $b = -3$ is 38.
Exercise 12.4
Question 1. Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
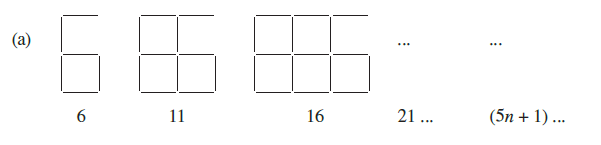
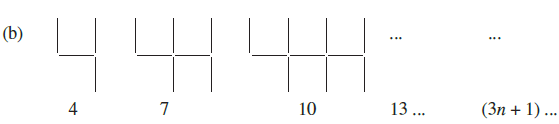
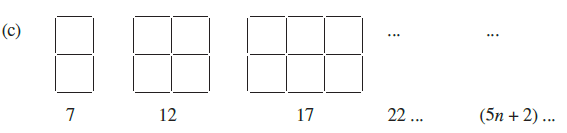
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern.
How many segments are required to form 5, 10, 100 digits of the kind
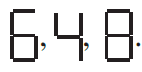
Answer:
Given
The algebraic expressions for the number of segments required to form $n$ digits of a certain kind are:
(a) For the digit '6': The expression is $5n + 1$.
(b) For the digit '4': The expression is $3n + 1$.
(c) For the digit '8': The expression is $5n + 2$.
To Find
The number of segments required to form $n=5$, $n=10$, and $n=100$ digits for each type (6, 4, and 8).
Solution
(a) For the digit '6' (Expression: $5n + 1$)
Substitute the given values of $n$ into the expression $5n + 1$.
For $n = 5$ digits:
Number of segments $= 5(5) + 1 = 25 + 1 = 26$.
For $n = 10$ digits:
Number of segments $= 5(10) + 1 = 50 + 1 = 51$.
For $n = 100$ digits:
Number of segments $= 5(100) + 1 = 500 + 1 = 501$.
(b) For the digit '4' (Expression: $3n + 1$)
Substitute the given values of $n$ into the expression $3n + 1$.
For $n = 5$ digits:
Number of segments $= 3(5) + 1 = 15 + 1 = 16$.
For $n = 10$ digits:
Number of segments $= 3(10) + 1 = 30 + 1 = 31$.
For $n = 100$ digits:
Number of segments $= 3(100) + 1 = 300 + 1 = 301$.
(c) For the digit '8' (Expression: $5n + 2$)
Substitute the given values of $n$ into the expression $5n + 2$.
For $n = 5$ digits:
Number of segments $= 5(5) + 2 = 25 + 2 = 27$.
For $n = 10$ digits:
Number of segments $= 5(10) + 2 = 50 + 2 = 52$.
For $n = 100$ digits:
Number of segments $= 5(100) + 2 = 500 + 2 = 502$.
Summary Table:
| Digit Type | Expression | Segments for 5 digits ($n=5$) | Segments for 10 digits ($n=10$) | Segments for 100 digits ($n=100$) |
| 6 | $5n + 1$ | 26 | 51 | 501 |
| 4 | $3n + 1$ | 16 | 31 | 301 |
| 8 | $5n + 2$ | 27 | 52 | 502 |
Question 2. Use the given algebraic expression to complete the table of number patterns.
| S. No. | Expression | Terms | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | ... | 10th | ... | 100th | ... | ||
| (i) | $2n – 1$ | 1 | 3 | 5 | 7 | 9 | - | 19 | - | - | - |
| (ii) | $3n + 2$ | 5 | 8 | 11 | 14 | - | - | - | - | - | - |
| (iii) | $4n + 1$ | 5 | 9 | 13 | 17 | - | - | - | - | - | - |
| (iv) | $7n + 20$ | 27 | 34 | 41 | 48 | - | - | - | - | - | - |
| (v) | $n^2 + 1$ | 2 | 5 | 10 | 17 | - | - | - | - | 10,001 | - |
Answer:
To complete the table, we substitute the term number ($n = 1, 2, 3, 4, 5, 10, 100$) into the given algebraic expression for each row.
(i) Expression: $2n - 1$
For $n=5$: $2(5) - 1 = 10 - 1 = 9$.
For $n=10$: $2(10) - 1 = 20 - 1 = 19$.
For $n=100$: $2(100) - 1 = 200 - 1 = 199$.
(ii) Expression: $3n + 2$
For $n=5$: $3(5) + 2 = 15 + 2 = 17$.
For $n=10$: $3(10) + 2 = 30 + 2 = 32$.
For $n=100$: $3(100) + 2 = 300 + 2 = 302$.
(iii) Expression: $4n + 1$
For $n=5$: $4(5) + 1 = 20 + 1 = 21$.
For $n=10$: $4(10) + 1 = 40 + 1 = 41$.
For $n=100$: $4(100) + 1 = 400 + 1 = 401$.
(iv) Expression: $7n + 20$
For $n=5$: $7(5) + 20 = 35 + 20 = 55$.
For $n=10$: $7(10) + 20 = 70 + 20 = 90$.
For $n=100$: $7(100) + 20 = 700 + 20 = 720$.
(v) Expression: $n^2 + 1$
For $n=5$: $(5)^2 + 1 = 25 + 1 = 26$.
For $n=10$: $(10)^2 + 1 = 100 + 1 = 101$.
For $n=100$: $(100)^2 + 1 = 10000 + 1 = 10001$.
The completed table is as follows:
| S. No. | Expression | Terms | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | ... | 10th | ... | 100th | ... | ||
| (i) | $2n – 1$ | 1 | 3 | 5 | 7 | 9 | ... | 19 | ... | 199 | ... |
| (ii) | $3n + 2$ | 5 | 8 | 11 | 14 | 17 | ... | 32 | ... | 302 | ... |
| (iii) | $4n + 1$ | 5 | 9 | 13 | 17 | 21 | ... | 41 | ... | 401 | ... |
| (iv) | $7n + 20$ | 27 | 34 | 41 | 48 | 55 | ... | 90 | ... | 720 | ... |
| (v) | $n^2 + 1$ | 2 | 5 | 10 | 17 | 26 | ... | 101 | ... | 10,001 | ... |

